Today, I am going to tell you a story of a Philosopher, Mr.Mathematics. He is a philosopher of calculation. He is as old as the sun or the moon. With his philosophy, we measure distance, predict the basics of time. His wife is Lady Calculation. She is intellectual, smart and honest. Now I know you want to know their sons. They have two sons, Arithmetic and Algebra.
Arithmetic knows what is known and solves the philosophy of addition, subtraction, Multiplication, and Division. So we may say that he can solve 5+6=?.
Algebra the younger sons with the power of his mother he replaces the known by alphabets. So we may say that he can solve x+y=?.
I know you all are looking on who is that young girl, she is Matrix. The Daughter of Algebra. Actually, Algebra has one Daughter and three sons Vector, Scalar and Tensor.
Vector: He is expert in managing the things with magnitude and direction.
Scalar: He is like the vector but inefficient in managing the things in a direction.
Tensor: He is having the power of vector and matrix.
Algebra has one more power, he can help in visualizing the things by using its Linear or Quadratic equations.
So let us start with some coding. We have two matrices as shown in below code we try to add both the matrix.
#A matrix Addition from mpl_toolkits.mplot3d import Axes3D import numpy as np import matplotlib.pyplot as plt fig = plt.figure() ax = fig.gca(projection='3d') # Plot the first line x1 = [0,6] y1 = [0,12] ax.plot(x1, y1, zs=0, zdir='z', label='curve in (x,y)') # Plot the second line x2 = [0,0] y2 = [0,14] ax.plot(x2, y2, zs=0, zdir='z', label='curve in (x,y)') #plot the third line x3 = np.array(x1)+np.array(x2) y3 = np.array(y1)+np.array(y2) ax.plot(x3,y3, zs=0, zdir='z', label='curve in (x,y)') plt.show()
#plot the third line fig = plt.figure() ax = fig.gca(projection='3d') x1 = [0,16] y1 = [0,12] ax.plot(x1, y1, zs=0, zdir='z', label='curve in (x,y)') # Plot the second line x2 = [0,1] y2 = [0,11] ax.plot(x2, y2, zs=0, zdir='z', label='curve in (x,y)') x4 = np.dot([16,22],[1,11]) ax.plot([0,0],[0,258], zs=0, zdir='z', label='curve in (x,y)') plt.show()
 The Family of Philosopher
The Family of Philosopher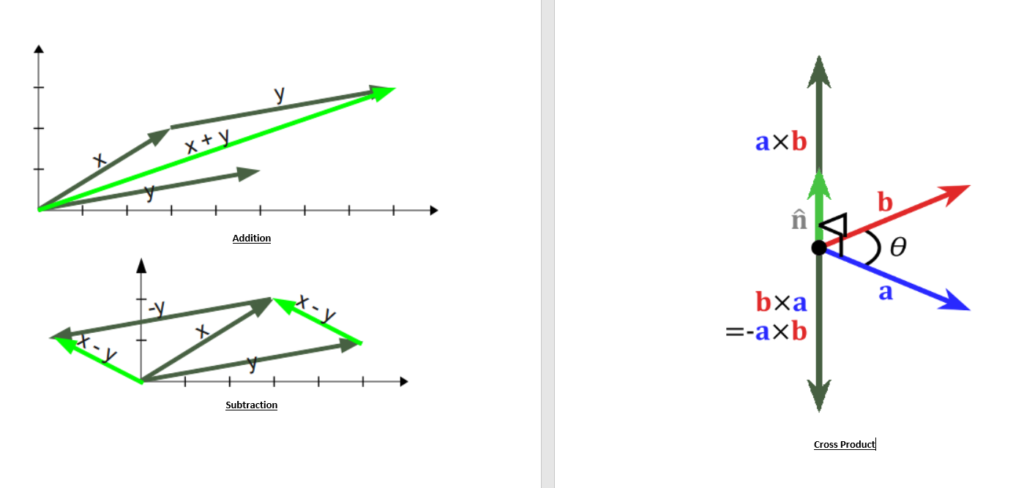
Very nice it is..