Decision Trees (DTs) are a non-parametric supervised learning method used for classification and regression. It works for both categorical and continuous input and output variables. It is a non-parametric algorithm. It uses the following algorithms.
1- ID3: ID3 uses Entropy and Information gain to construct a decision tree.
2- Gini Index (, if we select two items from a population at random then they must be of the same class, and probability for this is 1 if the population is pure.)
3- Chi-Square: Chi-square = ((Actual – Expected)^2 / Expected)^1/2
4- Reduction in Variance
Code in python:
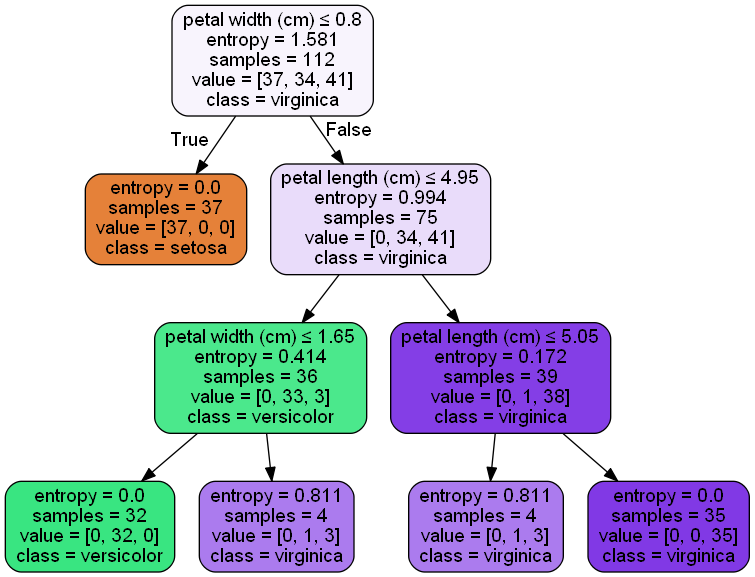
#Load Libraries import numpy as np import pandas as pd from sklearn.datasets import load_iris from sklearn.tree import DecisionTreeClassifier from sklearn.cross_validation import train_test_split from sklearn import metrics #import graphviz from sklearn import tree import matplotlib.pyplot as plt #Load Data from iris data iris = load_iris() X = iris.data y= iris.target X_train, X_test, y_train, y_test = train_test_split(X,y,random_state=0) DT = DecisionTreeClassifier(random_state=0) DT.fit(X_train,y_train) DT.predict(X_test) DT = DecisionTreeClassifier(criterion='entropy', random_state=0) DT.fit(X_train,y_train) DT.predict(X_test) metrics.accuracy_score(y_test,DT.predict(X_test))
Save a dot file:
import graphviz
import sys
from sklearn import tree
dot = tree.export_graphviz(DT,out_file=None,feature_names=iris.feature_names, class_names=iris.target_names, filled=True,rounded=True, special_characters=True)
graph = graphviz.Source(dot)
graph.format = 'png'
graph.render('iris1',view=True)Convert the dot file to graphiz.
dot -Tps filename.dot -o outfile.ps
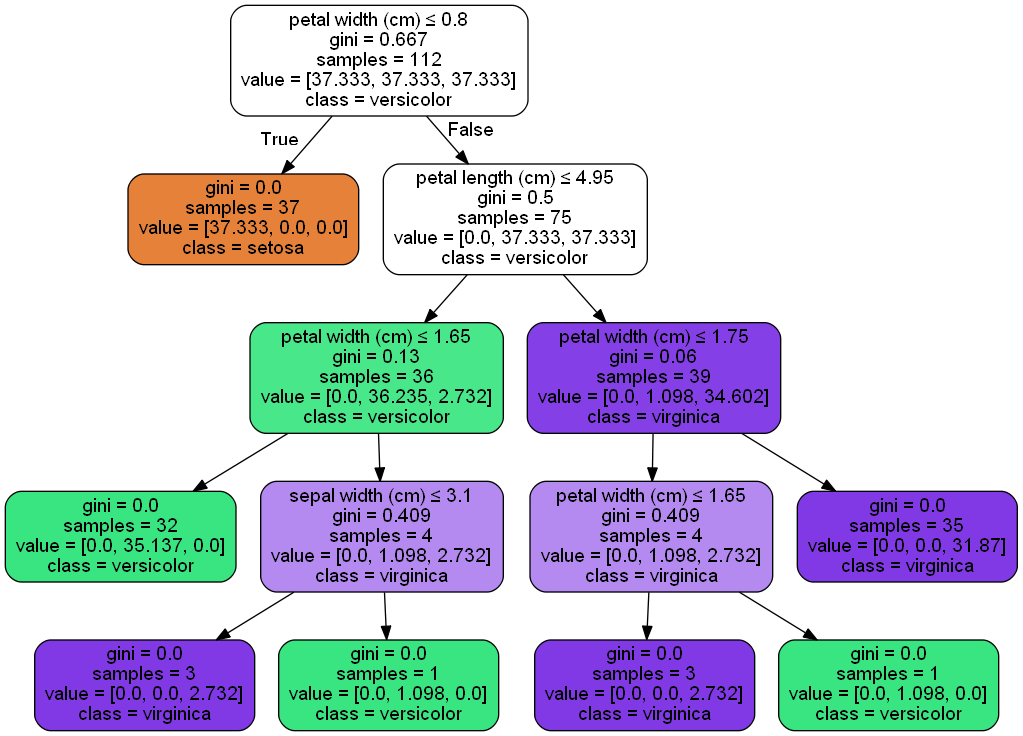
If we use the criterion as gini
DT = DecisionTreeClassifier(criterion='gini',min_samples_split=4,random_state=0) DT.fit(X_train,y_train) DT.predict(X_test) metrics.accuracy_score(y_test,DT.predict(X_test)) #Decision Tree: iris_gini_Default
Accuracy:
0.97368421052631582
Note:
Decision tree works on recursive partitioning, in which pure attributes takes the position of the top node. Impurity is calculated using the entropy of data in a node. If the data is totally homogenous entropy is 0 and if it is not entropy is 1.
the formula of Entropy :
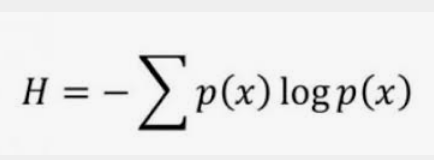
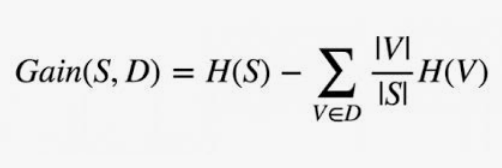
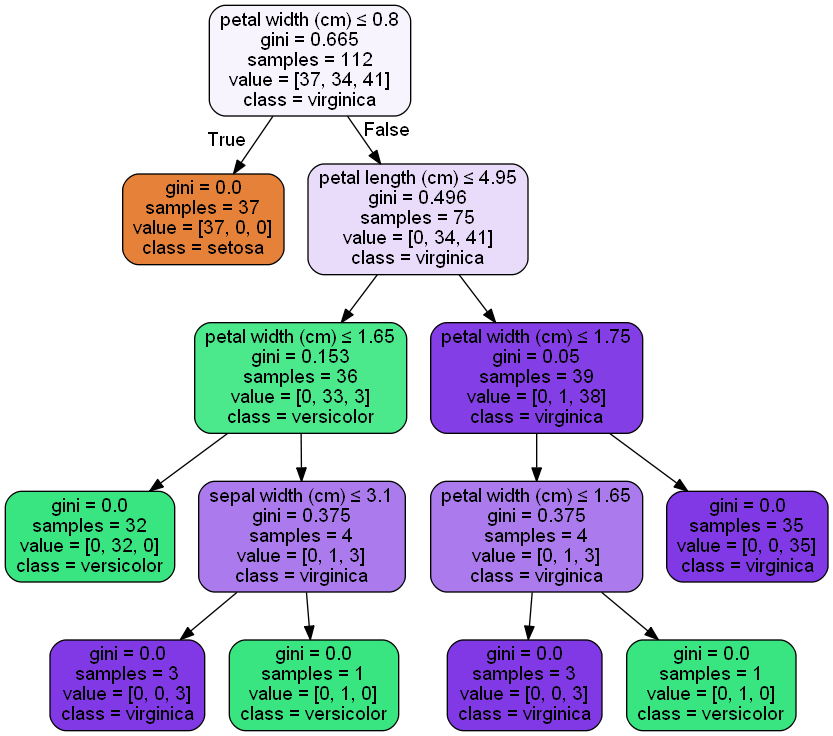
DT = DecisionTreeClassifier(class_weight='balanced',criterion='gini',min_samples_split=4,random_state=0) DT.fit(X_train,y_train) DT.predict(X_test) metrics.accuracy_score(y_test,DT.predict(X_test)) #Decision Tree: iris_gini_weight_Balanced dot_data = tree.export_graphviz(DT, out_file='iris_gini_weight_Balanced.dot')
DT = DecisionTreeClassifier(class_weight='balanced',criterion='entropy',min_samples_split=4,random_state=0) DT.fit(X_train,y_train) DT.predict(X_test) metrics.accuracy_score(y_test,DT.predict(X_test)) #Decision Tree: iris_entropy_weight_Balanced dot_data = tree.export_graphviz(DT, out_file='iris_entropy_weight_Balanced.dot')
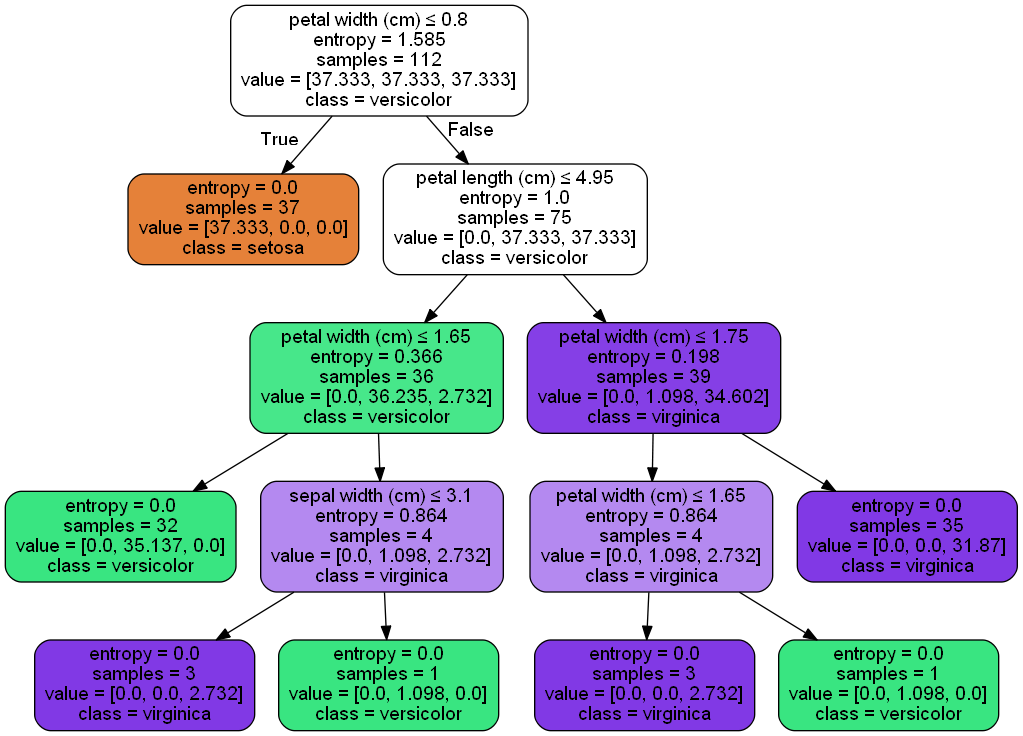
DT = DecisionTreeClassifier(criterion='entropy',max_depth=3, random_state=0) DT.fit(X_train,y_train) DT.predict(X_test) metrics.accuracy_score(y_test,DT.predict(X_test)) #Decision Tree: iris_entropy_MaxDepth dot_data = tree.export_graphviz(DT, out_file='iris_entropy_MaxDepth.dot')
When the Tree-based model performs better:
- If the relationship between dependent & independent variables is well approximated by a linear model, linear regression will outperform the tree-based model.
- If there is a high non-linearity & complex relationship between dependent & independent variables, a tree model will outperform a classical regression method.
- If you need to build a model that is easy to explain to people, a decision tree model will always do better than a linear model. Decision tree models are even simpler to interpret than linear regression!
Some advantages of decision trees are:
- Simple to understand and to interpret. Trees can be visualized.
- It requires little data preparation. Other techniques often require data normalization, dummy variables need to be created and blank values to be removed. Note however that this module does not support missing values.
- The cost of using the tree (i.e., predicting data) is logarithmic in the number of data points used to train the tree.
- Able to handle both numerical and categorical data. Other techniques are usually specialized in analyzing datasets that have only one type of variable. See the algorithms for more information.
- Able to handle multi-output problems.
- Uses a white-box model. If a given situation is observable in a model, the explanation for the condition is easily explained by boolean logic. By contrast, in a black-box model (e.g., in an artificial neural network), results may be more difficult to interpret.
- Possible to validate a model using statistical tests. That makes it possible to account for the reliability of the model.
- Performs well even if its assumptions are somewhat violated by the true model from which the data were generated.
The disadvantages of decision trees include:
- Decision-tree learners can create over-complex trees that do not generalize the data well. This is called overfitting. Mechanisms such as pruning (not currently supported), setting the minimum number of samples required at a leaf node, or setting the maximum depth of the tree is necessary to avoid this problem.
- Decision trees can be unstable because small variations in the data might result in a completely different tree being generated. This problem is mitigated by using decision trees within an ensemble.
References: