Different types of Activation functions in Deep Learning.

Activation functions

What is Activation function: It is a transfer function that is used to map the output of one layer to another. In daily life when we think every detailed decision is based on the results of small things. let’s assume the game of chess, every movement is based on 0 or 1. So in every move, we use the activation function. There are main following categories of functions

• Unipolar Binary
• Bipolar Binary
• Unipolar Continuous
• Bipolar Continuous
• Linear

linear

A straight line function where activation is proportional to input ( which is the weighted sum from neuron ).

This way, it gives a range of activations, so it is not binary activation. We can definitely connect a few neurons together and if more than 1 fires, we could take the max ( or softmax) and decide based on that. So that is ok too. Then what is the problem with this?

If you are familiar with gradient descent for training, you would notice that for this function, the derivative is a constant.

A = cx, derivative with respect to x is c. That means the gradient has no relationship with X. If there is an error in prediction, the changes made by backpropagation is constant and not depending on the change in input delta(x) !!!

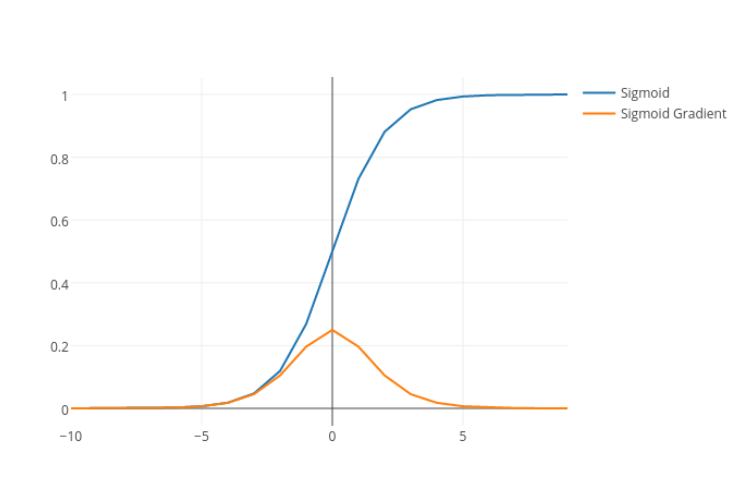
sigmoid

The Sigmoid function takes  any range real number and returns the output value which falls in the range of 0 to 1. Based on the convention we can expect the output value in the range of -1 to 1.

The sigmoid function produces the curve which will be in the Shape “S.” These curves used in the statistics too. With the cumulative distribution function (The output will range from 0 to 1).The main disadvantage of sigmoid is it stop learning for large value of x or in other words function get saturated for large value of x.

array([[ 0.73399752,  0.73419272,  0.73438782,  0.73458284,  0.73477777],
       [ 0.73885001,  0.73952477,  0.7401984 ,  0.7408709 ,  0.74154227],
       [ 0.74364489,  0.74478704,  0.74592584,  0.74706129,  0.74819337],
       [ 0.74838172,  0.74997895,  0.7515694 ,  0.75315306,  0.75472992],
       [ 0.75306009,  0.75509996,  0.75712841,  0.75914542,  0.76115096]])

softmax

The main advantage of using Softmax is the output probabilities range. The range will 0 to 1, and the sum of all the probabilities will be equal to one. If the softmax function used for multi-classification model it returns the probabilities of each class and the target class will have the high probability.

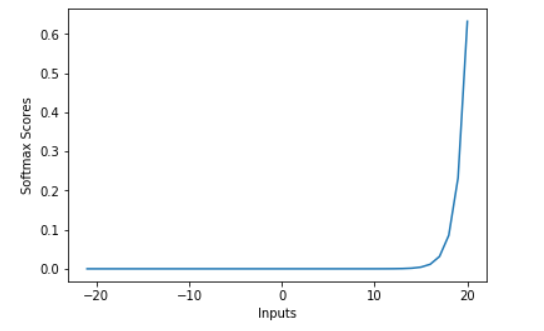
We can do a 2-d demonstration by using the following code:

x=np.arange(-2.0,6.0,0.1)
scores=np.vstack([x,np.ones_like(x),2*np.ones_like(x)])
print(scores.argmax())
plt.plot(x,softmax(scores).T,linewidth=0.7)
plt.show()

tanh

The tanh function, a.k.a. hyperbolic tangent function, is a rescaling of the logistic sigmoid, such that its outputs range from -1 to 1. (There’s horizontal stretching as well.).

The (-1,+1) output range tends to be more convenient for neural networks, so tanh functions show up there a lot. This functions are prone to reaching a point from where the gradient of the functions does not change or stop learning or it get saturated for large value of x.

relu

The Rectified Linear Unit- Relu has a great advantage over sigmod and tanh as it never gets saturated with high value of x. But the main disadvantage of this is its mean is not zero due to which the function becomes zero and overall learning is too slow.

But the issue is that all the negative values become zero immediately which decreases the ability of the model to fit or train from the data properly. That means any negative input given to the ReLU activation function turns the value into zero immediately in the graph, which in turns affects the resulting graph by not mapping the negative values appropriately.

“Unfortunately, ReLU units can be fragile during training and can “die”. For example, a large gradient flowing through a ReLU neuron could cause the weights to update in such a way that the neuron will never activate on any data point again.

Programmatically,

def reluDerivative(x):
     x[x<=0] = 0
     x[x>0] = 1
     return x

z = np.random.uniform(-1, 1, (3,3))

print(z)

reluDerivative(z)

[[-0.37386542  0.16629877 -0.74344915]
 [ 0.36153638 -0.0906727  -0.7030014 ]
 [-0.95665917  0.90534339  0.1792306 ]]

array([[0., 1., 0.],
       [1., 0., 0.],
       [0., 1., 1.]])

Once a ReLU ends up in this state, it is unlikely to recover, because the function gradient at 0 is also 0, so gradient descent learning will not maximize the weights. “Leaky” ReLUs with a small positive gradient for negative inputs (y=0.01x when x < 0 say) are one attempt to address this issue and give a chance to recover.

The sigmoid and tanh neurons can suffer from similar problems as their values saturate, but there is always at least a small gradient allowing them to recover in the long term.

refer

Leaky ReLU

It is an attempt to solve the dying ReLU problem

Swish

This function is introduced by Google it is a non -monotonic function. It provides better performance than Relu and Leaky Relu.

elu

ELU(Exponential linear unit) function solves the Vanishing gradient problem. The other mentioned activation functions are prone to reaching a point from where the gradient of the functions does not change or stop learning. The Elu tries to minimize the problem of relu and minimize the mean to zero so that the learning rate increases. Like batch normalization, ELUs push the mean towards zero,
but with a significantly smaller computational footprint.

selu

SELU is some kind of ELU but with a little twist.
α and λ are two fixed parameters, meaning we don’t backpropagate through them and they are not hyperparameters to make decisions about.

def selu(x):
    """Scaled Exponential Linear Unit. (Klambauer et al., 2017)
    # Arguments
        x: A tensor or variable to compute the activation function for.
    # References
        - [Self-Normalizing Neural Networks](https://arxiv.org/abs/1706.02515)
    """
    alpha = 1.6732632423543772848170429916717
    scale = 1.0507009873554804934193349852946
    return scale * elu(x, alpha)

For standard scaled inputs (mean 0, stddev 1), the values are α=1.6732~, λ=1.0507~.

softplus

Both the ReLU and Softplus are largely similar, except near 0 where the softplus is enticingly smooth and differentiable. It’s much easier and efficient to compute ReLU and its derivative than for the softplus function which has log(.) and exp(.) in its formulation. Interestingly, the derivative of the softplus function is the logistic function: f′(x)=11+e−xf′(x)=11+e−x.

In deep learning, computing the activation function and its derivative is as frequent as addition and subtraction in arithmetic. By switching to ReLU, the forward and backward passes are much faster while retaining the non-linear nature of the activation function required for deep neural networks to be useful.

softsign

The soft sign function is another nonlinearity which can be considered an alternative to tanh since it too does not saturate as easily as hard clipped functions

hard_sigmoid

σ is the “hard sigmoid” function: σ(x) = clip((x + 1)/2, 0, 1) = max(0, min(1, (x + 1)/2))

The intent is to provide a probability value (hence constraining it to be between 0 and 1) for use in stochastic binarization of neural network parameters (e.g. weight, activation, gradient). You use the probability p = σ(x) returned from the hard sigmoid function to set the parameter x to +1with p probability, or -1 with probability 1-p

References:

PDF for functions

A nice Question