Heteroscedasticity refers to the condition in which the variability of a variable is unequal across the range of values of a second variable that predicts it.
A scatterplot of these variables will often create a cone-like shape, as the scatter (or variability) of the dependent variable (DV) widens or narrows as the value of the independent variable (IV) increases.
note: The inverse of heteroscedasticity is homoscedasticity, which indicates that a DV’s variability is equal across values of an IV.
You can also visualize that it will be difficult to find the hypothesis in the below scenario.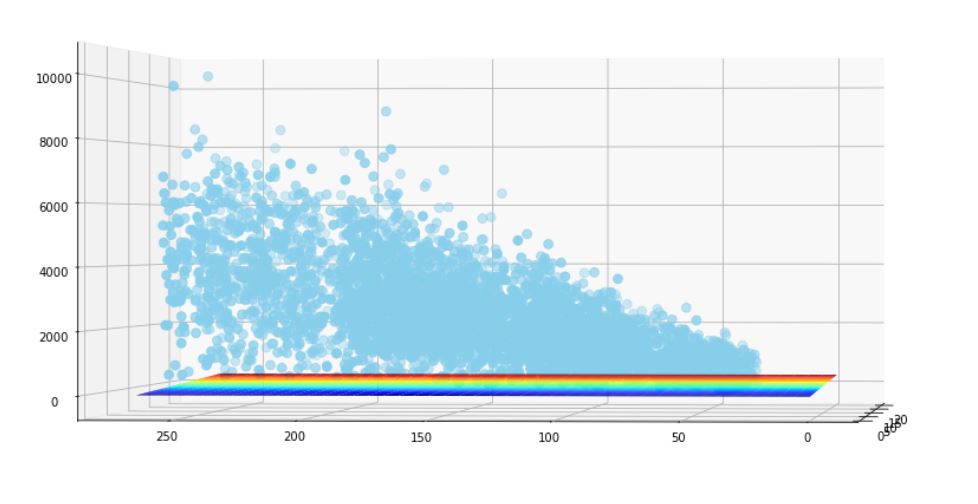
Using the log transformation can be a good approach to correct for heteroskedasticity, but only if all your values are positive and the new model provides a reasonable interpretation. Heteroskedasticity does not bias our coefficient estimates; it only makes our standard errors incorrect. Hence, if you only care about the fit of the model, then heteroskedasticity doesn’t matter.
You can get a more efficient model (i.e., one with smaller standard errors) if you use weighted least squares.
