KNN is another supervised classification technique, which makes no assumption of distribution of data. It is a non-parametric algorithm.It is the simplest technique of classification, the algorithm used for this technique is as:
Algorithm
Let m be the number of training data samples. Let p be an unknown point.
- Store the training samples in an array of data points in an array[]. This means each element of this array represents a tuple (x, y).
-
for i=0 to m: Calculate Euclidean distance d(arr[i], p).
- Make set S of K smallest distances obtained. Each of these distances corresponds to an already classified data point.
- Return the majority label among S.
Note K will be kept as minimum 3 and this will be kept as odd in number so that polling will always give us a significant result.
As this algorithm always uses the nearest neighbor in order to identify a new member thus it never makes a generalized model and hence it is also famous as a name of Lazy Learner.
Using Open CV we may write the following snippet of code:
import cv2 import numpy as np import matplotlib.pyplot as plt # Feature set containing (x,y) values of 25 known/training data trainData = np.random.randint(0,100,(25,2)).astype(np.float32) # Labels each one either Red or Blue with numbers 0 and 1 responses = np.random.randint(0,2,(25,1)).astype(np.float32) # Take Red families and plot them red = trainData[responses.ravel()==0] plt.scatter(red[:,0],red[:,1],80,'r','^') # Take Blue families and plot them blue = trainData[responses.ravel()==1] plt.scatter(blue[:,0],blue[:,1],80,'b','s') plt.show()
Output:
newcomer = np.random.randint(0,100,(1,2)).astype(np.float32)
plt.scatter(newcomer[:,0],newcomer[:,1],80,'b','s')
knn = cv2.ml.KNearest_create()
knn.train(trainData,cv2.ml.ROW_SAMPLE,responses)
ret, results, neighbours, dist = knn.findNearest(newcomer, 3)
print ("result: ", results,"\n")
print ("neighbours: ", neighbours,"\n")
print ("distance: ", dist)
plt.show()
Thus result shows all neighbours are from blue(1), thus it belongs to blue class:
We can solve the same problem using the SKLearn library:
X = [[10],[20],[20],[10],[20],[10],[20],[10],[10],] y = [1,1,2,2,1,2,1,1,1] from sklearn.neighbors import KNeighborsClassifier neigh = KNeighborsClassifier(n_neighbors=3) neigh.fit(X, y) print(neigh.predict([[4]])) print(neigh.predict_proba([[0.9]]))
Output:
[2] [[ 0.33333333 0.66666667]]
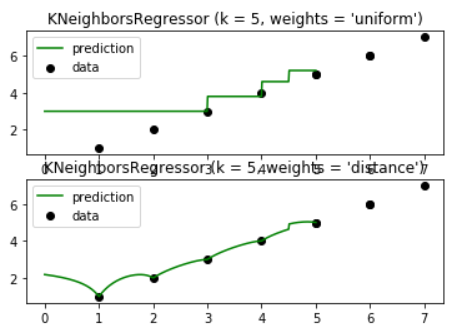
KNN also helps in solving regression problems, Using Sklearn we have following code snippet:
import numpy as np import matplotlib.pyplot as plt from sklearn import neighbors np.random.seed(0) X = [[1],[2],[3],[4],[5],[6],[7],[6],[5],] T = np.linspace(0, 5, 500)[:, np.newaxis] y = [1,2,3,4,5,6,7,6,5] n_neighbors = 5
for i, weights in enumerate(['uniform', 'distance']):
knn = neighbors.KNeighborsRegressor(n_neighbors, weights=weights)
y_ = knn.fit(X, y).predict(T)
plt.autoscale=True
plt.subplot(2, 1, i + 1)
plt.scatter(X, y, c='k', label='data')
plt.plot(T, y_, c='g', label='prediction')
plt.legend()
plt.title("KNeighborsRegressor (k = %i, weights = '%s')" % (n_neighbors,
weights))
plt.show()
Always Remember:
1. k-NN algorithm can be used for imputing the missing value of both categorical and continuous variables.
2. k-NN performs much better if all of the data have the same scale.
3. k-NN works well with a small number of input variables (p) but struggles when the number of inputs is very large.
4. k-NN makes no assumptions about the functional form of the problem is solved.
5. We can also use k-NN for regression problems. In this case, the prediction can be based on the mean or the median of the k-most similar instances.
6. Euclidean and Manhattan distances are used in case of continuous variables, whereas hamming distance is used in case of the categorical variable.
7. When you increase the k the bias will increase.
8. When you decrease the k the variance will increases.
9. A simple model has high biased and low variance.
References:
https://www.python-course.eu/k_nearest_neighbor_classifier.php
http://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html#sklearn.neighbors.KNeighborsClassifier
http://scikit-learn.org/stable/auto_examples/classification/plot_classifier_comparison.html#sphx-glr-auto-examples-classification-plot-classifier-comparison-py
Important: http://scikit-learn.org/stable/modules/classes.html#module-sklearn.neighbors