A Support Vector Machine is a supervised algorithm that can classify cases by finding a separator. SVM works by first mapping data to a high dimensional feature space so that data points can be categorized, even when the data are not otherwise linearly separable. Then, a separator is estimated for the data.
Lets X is an input feature and it is not linearly separable, then in this, we use a function ‘F’ over x so that the originally featured space is transformed into a new featured space. This will help us separate the training set into a linear separable space.
Usually, we map the data to high dimension featured space. While mapping this to a higher dimension the computation cost gets increased to a very high value so in order to minimize this, we use Kernel functions.

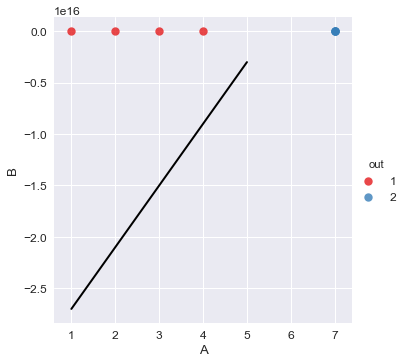
So, we can see when we transform the points to an appropriate space they will become linearly separable. There are certain types of feature transformation, that after the transformation the SVM can be solved efficiently, this brings us the Kernel Functions.
A Kernel function is defined as a function that corresponds to a dot product of two feature vector in some expanded feature space.
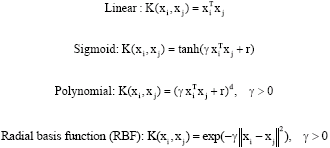
Python code:
import matplotlib.pyplot as plt <br>import pandas as pd import seaborn as sns; sns.set(font_scale=1.2) import matplotlib.pyplot as plt %matplotlib inline from sklearn import svm
#Lets take two array x=[[1,2],[2,3],[3,4],[4,5],[7,3],[7,4],[7,5],[7,5]] y=[1,1,1,1,2,2,2,2]
Create a Dataframe,
df=pd.DataFrame.from_records(x,columns=['A','B']) df['out']=y
model =svm.SVC(kernel='linear') model.fit(x,y) p=[3,4] d=model.predict([[3,4]]) output: 1
w=model.coef_[0]
a=-w[0]/w[1]<br>
xx=np.linspace(1,5)
yy=a*xx-(model.intercept_[0])/w[1]
#plot the supporting lines
b=model.support_vectors_[0]
y_down=a*xx+(b[1]-a*b[0])
b=model.support_vectors_[-1]
y_up=a*xx+(b[1]-a*b[0])
sns.lmplot('A','B',data=df,hue='out',palette='Set1',fit_reg=False,scatter_kws={"s":70})
plt.plot(xx,yy,linewidth=2,color='black')